Buscar este blog
Debes pensar en tu futuro, en el futuro de organización y en el futuro de tu comunidad. En este blog te acercamos a la prospectiva y el pensamiento estratégico, a la tecnología para tu vida y tus propositos, ofreciendote herramientas para construir un futuro deseado, sostenible y colectivo. Artículos sobre prospectiva, innovación, transformación digital, tecnología, finanzas, internacionalización, direccionamiento, planeación, organización empresarial, productividad, teorias y métodos.
Luego te recomiendo leer:
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Modelos de Ecuaciones Estructurales (SEM - Structural Equation Modeling)
Este post hace parte del tema Teoría de la Investigación.
Modelos de Ecuaciones Estructurales (SEM - Structural Equation Modeling)
Los Modelos de Ecuaciones Estructurales (SEM, por sus siglas en inglés de Structural Equation Modeling) son una poderosa técnica estadística utilizada para analizar relaciones complejas entre variables. Son especialmente útiles en las ciencias sociales, la administración, el management y otras áreas en las que los investigadores buscan estudiar patrones de relaciones causales entre múltiples variables. Los SEM combinan aspectos de análisis factorial y regresión múltiple, lo que permite a los investigadores modelar relaciones entre variables observadas y latentes de una manera más integral.
¿Qué son los Modelos de Ecuaciones Estructurales (SEM)?
Los Modelos de Ecuaciones Estructurales son una extensión de los modelos de regresión multivariante que permiten probar y estimar relaciones causales entre varias variables al mismo tiempo. A diferencia de los modelos de regresión estándar, los SEM permiten analizar tanto las relaciones directas como las indirectas entre variables, y también permiten modelar variables latentes, que son constructos no observados que se miden a través de varias variables observables (indicadores).
Los SEM se utilizan para probar hipótesis complejas en las que existen interdependencias entre variables, permitiendo un análisis más profundo de las relaciones entre múltiples variables al mismo tiempo. Son ampliamente utilizados en el campo del management y las ciencias sociales para el análisis de encuestas, experimentos y otros tipos de datos observacionales.
Componentes Clave de los SEM
Los modelos de ecuaciones estructurales combinan dos modelos subyacentes:
Modelo de Medida:
- Este modelo especifica cómo las variables latentes se relacionan con las variables observadas (indicadores). Las variables latentes son constructos teóricos que no se pueden medir directamente, como la satisfacción del cliente, el liderazgo o el compromiso organizacional. Para medir estas variables, se utilizan indicadores observables.
- El análisis factorial confirmatorio (CFA, por sus siglas en inglés de Confirmatory Factor Analysis) es una técnica dentro de los SEM que ayuda a establecer si los indicadores observados cargan adecuadamente sobre las variables latentes esperadas.
Modelo Estructural:
- Este modelo especifica las relaciones entre las variables latentes. Estas relaciones son a menudo causales y pueden incluir relaciones directas e indirectas. El modelo estructural muestra cómo las variables latentes afectan entre sí y cómo influyen en las variables observadas.
En términos generales, los SEM constan de:
- Variables exógenas: Variables independientes que no son explicadas por otras variables en el modelo.
- Variables endógenas: Variables dependientes que son explicadas o influenciadas por otras variables dentro del modelo.
- Variables latentes: Constructos teóricos no medidos directamente, pero inferidos a partir de otras variables observadas.
- Variables observadas: Indicadores medidos directamente que representan las variables latentes.
Representación Matemática de los SEM
Un SEM generalmente consiste en varias ecuaciones estructurales que modelan las relaciones entre las variables observadas y latentes. Estas ecuaciones suelen presentarse de la siguiente forma:
Modelo de Medida:
- X=Λxξ+δ
- Y=Λyη+ε
Donde:
- X y Y son las matrices de las variables observadas (indicadores) que miden las variables latentes ξ y η.
- yson las matrices de cargas factoriales que vinculan las variables observadas con las latentes.
- yson los errores de medición.
Modelo Estructural:
- η=Bη+Γξ+ζ
Donde:
- es una matriz de variables endógenas.
- es la matriz de relaciones entre variables latentes endógenas.
- es la matriz de relaciones entre variables exógenasyendógenas
- representa los errores estructurales (residuos).
Pasos para Desarrollar un SEM
El proceso para construir y estimar un modelo de ecuaciones estructurales involucra varias etapas:
Especificación del Modelo:
- El primer paso consiste en desarrollar el modelo teórico que describa las relaciones entre las variables. En esta fase, el investigador utiliza teoría previa y literatura para especificar cómo las variables están relacionadas y si estas relaciones son directas o indirectas.
Identificación del Modelo:
- Un modelo SEM debe ser identificable, lo que significa que debe haber suficiente información en los datos para estimar de manera única todos los parámetros del modelo. Esto se asegura cuando el número de ecuaciones y restricciones en el modelo es suficiente para resolver el sistema.
Estimación del Modelo:
- Se utilizan varios métodos de estimación para calcular los parámetros del modelo, como el Método de Máxima Verosimilitud (ML), Máxima Verosimilitud Robusta o el método GLS (Generalized Least Squares). Estos métodos buscan ajustar el modelo teórico a los datos observados.
Evaluación del Modelo:
- La calidad del ajuste del modelo se evalúa mediante varios índices de ajuste, que indican qué tan bien se ajusta el modelo teórico a los datos observados. Algunos de los indicadores más comunes son:
- Chi-cuadrado: Evalúa la diferencia entre el modelo estimado y los datos observados. Un valor bajo sugiere un buen ajuste.
- RMSEA (Root Mean Square Error of Approximation): Un índice que indica cuánta discrepancia existe entre los datos y el modelo por cada grado de libertad. Un valor menor a 0.06 indica un buen ajuste.
- CFI (Comparative Fit Index) y TLI (Tucker-Lewis Index): Miden el ajuste relativo en comparación con un modelo nulo (sin relaciones). Valores por encima de 0.90 o 0.95 indican un buen ajuste.
- SRMR (Standardized Root Mean Square Residual): Un índice de ajuste absoluto que mide la diferencia entre las correlaciones observadas y las predichas.
Modificación del Modelo:
- Si el modelo inicial no tiene un buen ajuste, los investigadores pueden usar las modificaciones sugeridas (por ejemplo, liberar algunas restricciones en las relaciones entre las variables) para mejorar el ajuste del modelo a los datos.
Interpretación de los Resultados:
- Una vez que se ha estimado el modelo y se ha alcanzado un buen ajuste, se interpretan los coeficientes de las relaciones causales para entender cómo las variables influyen entre sí.
Ejemplo de Aplicación de los SEM en Management
En el campo del management, los Modelos de Ecuaciones Estructurales se utilizan con frecuencia para analizar constructos como el compromiso organizacional, la satisfacción laboral, el liderazgo, o la cultura organizacional, todos ellos variables latentes que no se pueden observar directamente.
Ejemplo:
Un investigador podría estar interesado en entender cómo el liderazgo transformacional (una variable latente) influye en la satisfacción laboral y el compromiso organizacional (también variables latentes). Para medir el liderazgo transformacional, el investigador podría utilizar una encuesta que incluye preguntas sobre la visión del líder, el apoyo emocional, la comunicación y la capacidad de inspirar. Cada una de estas preguntas sería una variable observada que mide el constructo latente de liderazgo.
En el modelo SEM:
Variables latentes:
- Liderazgo transformacional (medido a través de varios ítems observados).
- Satisfacción laboral.
- Compromiso organizacional.
Relaciones causales:
- Liderazgo transformacional → Satisfacción laboral.
- Liderazgo transformacional → Compromiso organizacional.
- Satisfacción laboral → Compromiso organizacional.
El investigador puede usar SEM para estimar los efectos directos e indirectos entre estas variables latentes, y determinar si el liderazgo transformacional influye directamente en el compromiso organizacional o si este efecto está mediado por la satisfacción laboral.
Fortalezas y Limitaciones de los SEM
Fortalezas
- Análisis de múltiples relaciones simultáneamente: A diferencia de los modelos de regresión simples, los SEM permiten estudiar múltiples relaciones entre variables al mismo tiempo, ofreciendo un análisis más completo.
- Incorporación de variables latentes: Los SEM permiten incluir variables que no pueden ser medidas directamente, lo que es crucial en el estudio de constructos psicológicos y organizacionales.
- Pruebas de mediación y moderación: Los SEM son herramientas útiles para analizar relaciones mediadas y moderadas entre variables, lo que proporciona una comprensión más matizada de los procesos causales.
- Flexibilidad: Pueden adaptarse a muchas estructuras de datos, como datos longitudinales o anidados, y pueden manejar tanto variables continuas como categóricas.
Limitaciones
- Dependencia de los supuestos: Los SEM requieren que se cumplan varios supuestos estadísticos, como la normalidad multivariada y la linealidad. Si estos supuestos no se cumplen, los resultados pueden ser incorrectos.
- Complejidad: Los SEM son complejos y requieren un conocimiento profundo tanto de la teoría subyacente como de las técnicas estadísticas, lo que puede ser un desafío para los investigadores menos experimentados.
- Sensibilidad a muestras pequeñas: Los SEM generalmente requieren muestras grandes para proporcionar estimaciones estables y precisas. Modelar con muestras pequeñas puede llevar a resultados erróneos.
Conclusión
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Entradas populares
Ejes de Peter Schwartz: Cómo construir escenarios estratégicos
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
¿Qué es la Prospectiva Estratégica?
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Elementos del Estudio Prospectivo Estratégico
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Análisis PESTAL
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Las mejores películas y series para aprender sobre estrategia, liderazgo y mucho más
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
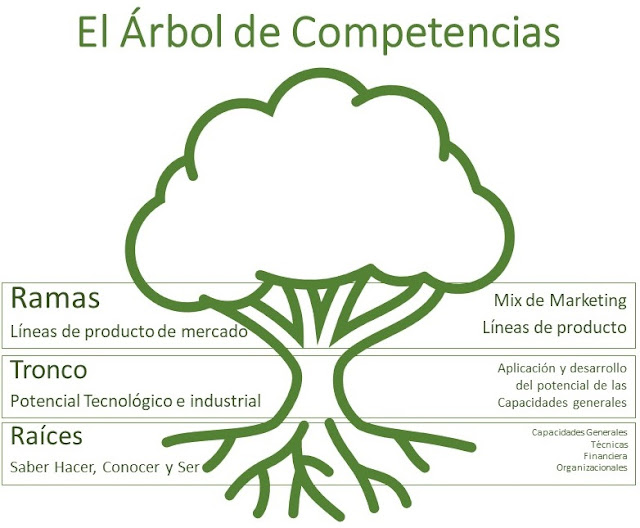
El Árbol de Competencias
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
¿Cuáles son las 10 tecnologías emergentes más importantes de 2023 y cuál será su impacto en el futuro?
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
La Teoría Basada en Recursos (Resource-Based View, RBV) de Jay B. Barney
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Prospectiva estratégica: Ejemplos y su aplicación en el mundo empresarial
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Método SMIC o Sistema de Matriz de Impacto Cruzado
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones










Comentarios
Publicar un comentario