Buscar este blog
Debes pensar en tu futuro, en el futuro de organización y en el futuro de tu comunidad. En este blog te acercamos a la prospectiva y el pensamiento estratégico, a la tecnología para tu vida y tus propositos, ofreciendote herramientas para construir un futuro deseado, sostenible y colectivo. Artículos sobre prospectiva, innovación, transformación digital, tecnología, finanzas, internacionalización, direccionamiento, planeación, organización empresarial, productividad, teorias y métodos.
Luego te recomiendo leer:
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
La Teoría de Juegos (Game Theory) de John von Neumann y Oskar Morgenstern
La Teoría de Juegos (Game Theory) de John von Neumann y Oskar Morgenstern
La Game Theory o Teoría de Juegos, desarrollada inicialmente por John von Neumann y Oskar Morgenstern en su obra seminal de 1944, "Theory of Games and Economic Behavior", es un marco matemático utilizado para analizar las interacciones estratégicas entre individuos o "jugadores" en situaciones en las que los resultados para cada participante dependen no solo de sus propias decisiones, sino también de las decisiones tomadas por los demás. En términos generales, la teoría de juegos estudia cómo los individuos o entidades toman decisiones estratégicas en entornos donde sus decisiones están interrelacionadas, y cómo esas interacciones conducen a diferentes resultados.
La Teoría de Juegos ha tenido un impacto profundo en múltiples campos, desde la economía y las ciencias políticas hasta la teoría organizacional y el comportamiento estratégico en los negocios. A continuación, te explico en detalle sus fundamentos, componentes clave, y aplicaciones en el campo de la administración y la organización.
Contexto y Origen de la Game Theory
La Game Theory surge como una respuesta a la necesidad de comprender las interacciones estratégicas en situaciones de conflicto y cooperación. Antes de la teoría de juegos, la economía clásica se centraba en el estudio del comportamiento individual sin tener en cuenta cómo las decisiones de una persona o entidad podían influir y ser influenciadas por las decisiones de otros.
John von Neumann, un matemático destacado, ya había desarrollado en 1928 un importante resultado conocido como el teorema minimax, que resolvía un tipo particular de juego llamado "juego de suma cero", en el que la ganancia de un jugador es exactamente igual a la pérdida de otro jugador. Oskar Morgenstern, un economista, colaboró con von Neumann en la creación de un marco teórico más amplio que pudiera aplicarse a una gama más amplia de situaciones estratégicas, dando lugar al texto clásico de 1944.
Fundamentos de la Game Theory
La Teoría de Juegos examina las decisiones estratégicas que toman individuos o entidades en situaciones donde las decisiones de uno afectan a los demás, y viceversa. Los principales componentes de la teoría incluyen:
Jugadores:
- En la teoría de juegos, los jugadores son los agentes o entidades que toman decisiones estratégicas. Los jugadores pueden ser individuos, empresas, organizaciones, países, etc. Cada jugador tiene un conjunto de posibles acciones o estrategias que puede elegir, y el resultado de estas elecciones depende de lo que hagan los demás jugadores.
Estrategias:
- Una estrategia es un plan de acción que un jugador puede seguir en un juego. Puede ser una elección puntual (en juegos simples) o un conjunto de decisiones condicionales (en juegos más complejos). Una estrategia puede ser:
- Estrategia pura: Una decisión específica que el jugador toma.
- Estrategia mixta: Una combinación probabilística de diferentes estrategias puras, lo que permite al jugador elegir entre varias estrategias con diferentes probabilidades.
Resultados (Payoffs):
- Los resultados o payoffs son las recompensas que los jugadores obtienen en función de las estrategias que ellos y los demás jugadores han elegido. Los payoffs pueden ser beneficios financieros, ganancias en bienestar, o cualquier otra forma de utilidad que motive a los jugadores.
Juegos de suma cero y no suma cero:
- Juegos de suma cero: Son aquellos en los que las ganancias de un jugador son exactamente iguales a las pérdidas de otro jugador. El total de payoffs en el juego siempre suma cero. Por ejemplo, en un juego de póker, lo que un jugador gana es igual a lo que los demás pierden.
- Juegos de no suma cero: Son aquellos en los que es posible que todos los jugadores ganen o pierdan simultáneamente. Aquí, la cooperación entre jugadores puede conducir a un mayor beneficio colectivo.
Información perfecta e imperfecta:
- Información perfecta: Se refiere a situaciones en las que todos los jugadores tienen acceso a la misma información sobre las decisiones anteriores y futuras de los demás. Un ejemplo clásico de juego de información perfecta es el ajedrez, donde todos los jugadores ven los movimientos anteriores.
- Información imperfecta: Se refiere a situaciones en las que los jugadores no tienen acceso completo a las decisiones o estrategias de los demás, lo que introduce incertidumbre. Esto es común en los negocios, donde las empresas no siempre saben qué decisiones tomarán sus competidores.
Equilibrio de Nash:
- El Equilibrio de Nash, propuesto por el matemático John Nash en 1950, es uno de los conceptos más importantes de la teoría de juegos. Se refiere a una situación en la que ningún jugador tiene un incentivo para cambiar su estrategia, dado lo que los demás jugadores están haciendo. En otras palabras, un equilibrio de Nash ocurre cuando todos los jugadores están eligiendo las mejores estrategias posibles, dadas las estrategias de los demás.
- En este equilibrio, todos los jugadores maximizan su beneficio dado el comportamiento de los demás, y no pueden mejorar sus resultados unilaterales cambiando de estrategia.
Tipos de Juegos en la Game Theory
Existen varios tipos de juegos que se estudian dentro de la Teoría de Juegos:
Juegos de suma cero:
- Como se mencionó, en estos juegos lo que un jugador gana es igual a lo que otro pierde. Los juegos de suma cero son altamente competitivos y no permiten la cooperación entre jugadores.
Juegos de no suma cero:
- En estos juegos, los jugadores pueden beneficiarse mutuamente de la cooperación o tomar decisiones que no perjudican directamente a los demás. Un ejemplo de juego no suma cero es el Dilema del Prisionero.
Juegos cooperativos y no cooperativos:
- Juegos cooperativos: En estos juegos, los jugadores pueden comunicarse y hacer acuerdos vinculantes para maximizar sus beneficios conjuntos. Se utilizan con frecuencia para estudiar coaliciones en política o alianzas empresariales.
- Juegos no cooperativos: Aquí, los jugadores no pueden hacer acuerdos vinculantes y deben actuar estratégicamente para maximizar su beneficio individual. Estos juegos son más competitivos y reflejan situaciones como la competencia empresarial.
Juegos secuenciales y simultáneos:
- Juegos secuenciales: En estos juegos, los jugadores toman decisiones en una secuencia temporal, donde uno juega después de ver la acción del otro. Un ejemplo es el ajedrez, donde los jugadores toman turnos.
- Juegos simultáneos: En estos juegos, los jugadores toman decisiones al mismo tiempo, sin saber lo que los demás harán. El Dilema del Prisionero es un juego simultáneo clásico.
Juegos de información completa e incompleta:
- Juegos de información completa: Los jugadores tienen acceso a toda la información relevante sobre el juego y las estrategias de los demás.
- Juegos de información incompleta: Los jugadores carecen de información sobre algunos aspectos del juego, como las estrategias disponibles para otros o los resultados potenciales.
Ejemplos Clásicos de la Teoría de Juegos
El Dilema del Prisionero:
- En este juego, dos prisioneros son arrestados y se les ofrece un trato. Si uno de los prisioneros traiciona al otro y el otro guarda silencio, el traidor será liberado y el otro será encarcelado por mucho tiempo. Si ambos traicionan, ambos recibirán una pena moderada. Si ambos guardan silencio, recibirán una pena leve. El dilema radica en que, aunque ambos estarían mejor cooperando (guardando silencio), la estrategia dominante para ambos es traicionar al otro, ya que maximiza el beneficio individual.
Este juego ilustra cómo las decisiones racionales individuales pueden llevar a un resultado subóptimo para todos.
El juego de la batalla de los sexos:
- Aquí, dos personas desean pasar la tarde juntos, pero tienen preferencias diferentes: uno prefiere el cine y el otro un partido de fútbol. Ambos prefieren estar juntos a estar separados, pero hay un conflicto sobre qué actividad realizar. El desafío es coordinarse para obtener el mejor resultado colectivo.
El juego del ultimátum:
- Un jugador recibe una cantidad de dinero y debe proponer cómo dividirla con otro jugador. El segundo jugador puede aceptar o rechazar la oferta. Si acepta, se realiza la división; si rechaza, ambos jugadores no reciben nada. Este juego pone de relieve cómo las expectativas de justicia y equidad influyen en la toma de decisiones, desafiando el comportamiento puramente racional.
Aplicación de la Game Theory en la Administración y las Organizaciones
La Teoría de Juegos ha sido ampliamente aplicada en el campo de la administración y la gestión empresarial, especialmente en la toma de decisiones estratégicas, la competencia entre empresas, la negociación, y la formación de coaliciones. Algunas de sus aplicaciones clave incluyen:
Competencia empresarial:
- Las empresas pueden usar la teoría de juegos para anticipar las acciones de sus competidores y formular estrategias óptimas. Por ejemplo, en una guerra de precios, las empresas pueden analizar las consecuencias de reducir precios y tratar de predecir las respuestas de sus competidores.
Negociación y toma de decisiones:
- En situaciones de negociación, la teoría de juegos ofrece un marco para analizar cómo se pueden alcanzar acuerdos mutuamente beneficiosos. Las empresas que están negociando contratos, fusiones o adquisiciones pueden utilizar estos principios para maximizar sus resultados.
Formación de alianzas y coaliciones:
- En entornos donde la cooperación es esencial para el éxito, la teoría de juegos permite a las organizaciones evaluar cuándo es ventajoso formar alianzas o coaliciones, y cómo dividir los beneficios generados.
Diseño de incentivos:
- Las organizaciones también pueden usar la teoría de juegos para diseñar sistemas de incentivos que alineen los intereses de los empleados, accionistas y otros stakeholders. Esto es particularmente útil en la creación de estructuras salariales o programas de bonificaciones.
Conclusión
La Teoría de Juegos de Von Neumann y Morgenstern es un marco revolucionario que ofrece herramientas para entender la toma de decisiones en situaciones estratégicas interdependientes. Aunque comenzó como una teoría matemática abstracta, sus aplicaciones prácticas son profundas y abarcan desde la economía hasta la política, la biología y la administración de empresas. La capacidad de predecir los comportamientos estratégicos de los demás y de anticipar los resultados de las interacciones es una habilidad crucial para cualquier líder organizacional, y la teoría de juegos proporciona una base sólida para desarrollar estas capacidades.
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Entradas populares
Ejes de Peter Schwartz: Cómo construir escenarios estratégicos
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
¿Qué es la Prospectiva Estratégica?
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Elementos del Estudio Prospectivo Estratégico
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Análisis PESTAL
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Las mejores películas y series para aprender sobre estrategia, liderazgo y mucho más
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
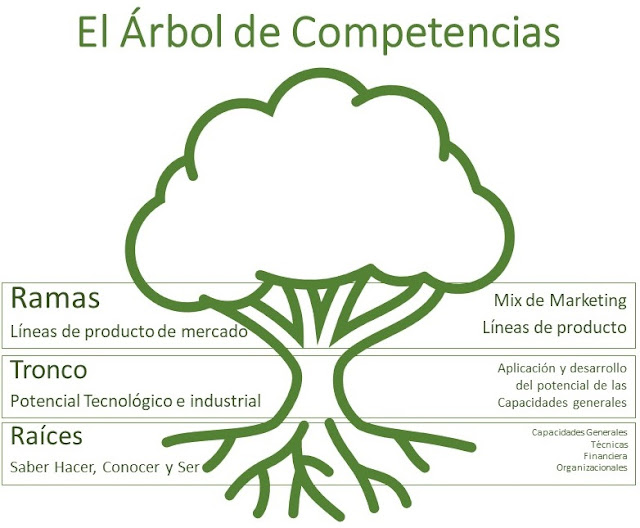
El Árbol de Competencias
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
¿Cuáles son las 10 tecnologías emergentes más importantes de 2023 y cuál será su impacto en el futuro?
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
La Teoría Basada en Recursos (Resource-Based View, RBV) de Jay B. Barney
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Prospectiva estratégica: Ejemplos y su aplicación en el mundo empresarial
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Método SMIC o Sistema de Matriz de Impacto Cruzado
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones









Comentarios
Publicar un comentario